问题
解答题
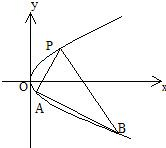
| 设P（x0，y0）是抛物线y2=2px（p＞0）上异于顶点的定点，A（x1，y1），B（x2，y2）是抛物线上的两个动点，且直线PA与PB的倾斜角互补 （1）求
（2）证明直线AB的斜率是非零常数． |
答案
（I）设直线PA的斜率为kPA，直线PB的斜率为k PB
由y12=2px1，y02=2px0
相减得（y1-y0）（y1+y0）=2p（x1-x0）
故 kPA=
=y1-y0 x1-x0
(x1≠x0)2p y1+y0
同理可得 kPB=
(x2≠x0)2p y2+y0
由PA，PB倾斜角互补知kPA=-kPB
即
=-2p y1+y0 2p y2+y0
所以y1+y2=-2y0
故
=-2y1+y2 y0
（II）设直线AB的斜率为kAB
由y22=2px2，y12=2px1
相减得（y2-y1）（y2+y1）=2p（x2-x1）
所以 kAB=
=y2-y1 x2-x1
(x1≠x2)2p y1+y2
将y1+y2=-2y0（y0＞0）代入得kAB=
=-2p y1+y2
，所以kAB是非零常数．p y0
