问题
问答题
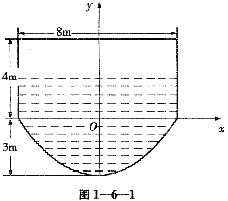
设一盛有某种液体的旋转形容器过旋转轴的剖面尺寸大小及坐标系的选择如图1-6-1所示.上部两边轮廓线为铅直线,下部轮廓线为抛物线,液体的比重为μ,原贮存液体深5m,现将该液体抽至容器口水平面处排出.试问欲使容器内液面下降4m,需做多少功
答案
参考答案:如图1-6-3,由题设,可令下半部剖面的抛物线方程为
[*]
x2=2p(y+3),-3≤y≤0.
当x=±4,y=0,得[*],于是抛物线方程为
[*]
因此,整体剖面轮廓线(右半部)的方程为
[*]
取y为积分变量,对应[y,y+dy]的一薄层液体的体积为dv=πx2dy,重量为
dP=μπx2dy.
将此薄层提升到容器口,经过的距离为4-y,于是提升该薄层液体需做功
dW=μπx2(4-y)dy.
根据题设,由原深5m到深1m,即相应地从原y=2到y=-2,因此
[*]
解析:
[分析]: 这是一道定积分的应用题.只要把所求功的微元找出来,再作积分即可.
