问题
解答题
| 台州椒江素有“中国被套绣衣之都”的美称,其产品畅销全球,某制造企业欲将n件产品运往A,B,C三地销售,要求运往C地的件数是运往A地件数的2倍,椒江运往A、B、C三地的运费分别是30元/件,8元/件,25元/件.设安排x件产品运往A地. (1)当n=200时,①根据信息填表:
(2)若总运费为5800元,求n的最小值. |
答案
(1)①根据信息填表:
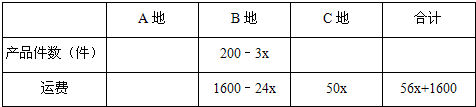 ;
;
②由题意,得
,200-3x≤2x① 30x+1600-24x+50x≤4000②
解不等式①得,x≥40,
解不等式②得,x≤42
,6 7
所以,40≤x≤42
,6 7
∵x为整数,
∴x=40或41或42,
∴有三种方案,分别是:方案一:A地40件,B地80件,C地80件;
方案二:A地41件,B地77件,C地82件;
方案三:A地42件,B地74件,C地84件;
(2)由题意,得30x+8(n-3x)+50x=5800,
整理,得n=725-7x,
∵n-3x≥0,
∴725-7x-3x≥0,
解得x≤72.5,
又∵x≥0,
∴0≤x≤72.5且x为整数,
∵n随x的增大而减少,
∴当x=72时,n有最小值为725-7×72=221.
