搜题请搜索小程序“爱下问搜题”
问题 选择题
已知抛物线y2=2px（p＞0）的焦点F与双曲
x2
4
-
y2
5
=1的右焦点重合，抛物线的准线与x轴的交点为K，点A在抛物线上且|AK|=
2
|AF|，则A点的横坐标为（　　）
A．2
2
B．3C．2
3
D．4
答案

∵双曲线

x2
4
-
y2
5
=1，其右焦点坐标为（3，0）．

∴抛物线C：y2=12x，准线为x=-3，
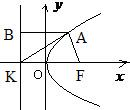
∴K（-3，0）
设A（x0，y0），过A点向准线作垂线AB，则B（-3，y0）
∵|AK|=

2
|AF|，又AF=AB=x0-（-3）=x0+3，
∴由BK2=AK2-AB2得BK2=AB2，从而y02=（x0+3）2，即12x0=（x0+3）2，

解得x0=3．

故选B．

综合题

（18分）阅读下列材料：

材料一   1921年3月，俄共（布）第十次代表大会召开，根据列宁的提议通过了实行新经济政策的决议。……当这消息被 * * 国际的各国代表得知时，有些外国革命者痛惜地哭叹道：“晓得今天是这样，我们错不该参加十月革命了。”还有人吼道：“列宁要把我们带到哪里去？”……西方人士却说：“俄国的这一招，是痛击我们的！”

材料二   “总统先生！”一位年轻的记者曾经问富兰克林•罗斯福：“你是 * * 党吗？”“不是。”“你是社会主义者吗？”“不是。”这位记者对罗斯福拒不承认自己属于那种常规的意识形态感到困惑，最后问道：“那你的哲学是什么？”“哲学？”有点迷惑不解的总统说，“哲学？我是基督教徒，是民主党人……如此而已。”

材料三  1946～1992年，法国政府连续实施了10个计划，规划经济发展方向，确定总体目标和长远战略：这些计划是指导性的，一些指标对企业，尤其是私有企业没有强制性，主要是为企业决策提供权威的信息和可靠的政策依据。政府采取激励措施来推动计划的实现。……戴高乐总统也曾说过，计划能补偿自由的缺点，而同时又不使它失去优点。

请回答：（1）材料一中列宁实行的新经济政策为什么让许多革命者感到“痛惜”？西方人士为什么说“俄国的这一招，是痛击我们的”呢？（６分）

（2）材料二中的记者为什么质问罗斯福是“ * * 党”是“社会主义者”呢？（４分）

（3）依据材料三说明法国政府是如何对经济进行干预的？你认为材料中“自由的缺点”及计划的“优点”各是什么？（６分）

（4）某中学历史兴趣小组决定围绕上述材料开展研究性学习，请你为他们拟订一个恰当的题目，要求紧扣材料内容。（２分）
查看答案
问答题 简答题

陶瓷的注浆成形有哪些？
查看答案