问题
解答题
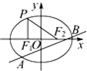
已知点P(-1,
(1)求椭圆E的方程; (2)设A、B是椭圆E上两个动点,是否存在λ,满足
|
答案
(1)∵PF1⊥x轴,
∴F1(-1,0),c=1,F2(1,0),
|PF2|=
=22+(
)23 2
,2a=|PF1|+|PF2|=4,a=2,b2=3,5 2
椭圆E的方程为:
+x2 4
=1;(4分)y2 3
(2)设A(x1,y1)、B(x2,y2),由
+PA
=λPB
得PO
(x1+1,y1-
)+(x2+1,y2-3 2
)=λ(1,-3 2
),3 2
所以x1+x2=λ-2,y1+y2=
(2-λ)①(5分)3 2
又3x12+4y12=12,3x22+4y22=12,
两式相减得3(x1+x2)(x1-x2)+4(y1+y2)(y1-y2)=0②
以①式代入可得AB的斜率k=
=y1-y2 x1-x2
(8分)1 2
设直线AB的方程为y=
x+t,1 2
与3x2+4y2=12联立消去y并整理得x2+tx+t2-3=0,
△=3(4-t2)>0,t∈(-2,2),x1+x2=-t=λ-2
点M到直线AB的距离为d=
=2|t| 5
,∴t=±5
∉(-2,2)(10分)5 2
∵t=2-λ∴λ=
或-9 4
不合题意.故这样的λ不存在(12分)1 2