问题
解答题
我们在下面的表格内填写数值：先将第1行的所有空格填上1；再把一个首项为1，公比为q的数列{an}依次填入第一列的空格内；然后按照“任意一格的数是它上面一格的数与它左边一格的数之和”的规则填写其它空格．
（2）设第3列的数依次为c1，c2，c3，…，cn，求证：对于任意非零实数q，c1+c3＞2c2； （3）请在以下两个问题中选择一个进行研究 （只能选择一个问题，如果都选，被认为选择了第一问）． ①能否找到q的值，使得（2）中的数列c1，c2，c3，…，cn的前m项c1，c2，…，cm （m≥3）成为等比数列？若能找到，m的值有多少个？若不能找到，说明理由． ②能否找到q的值，使得填完表格后，除第1列外，还有不同的两列数的前三项各自依次成等比数列？并说明理由． |
答案
（1）由题意得，B1=q，B2=1+q，
B3=1+（1+q）=2+q，…，Bn=（n-1）+q，
∴B1+B2+…+Bn=1+2+…+（n-1）+nq=
| n(n-1) |
| 2 |
（2）由题意得，c1=1，c2=1+（1+q）=2+q，
c3=(2+q)+(1+q+q2)=3+2q+q2，
由 c1+c3-2c2=1+3+2q+q2-2(2+q)=q2＞0，
即 c1+c3＞2c2．
（3）①先设c1，c2，c3成等比数列，由c1c3=
| c | 22 |
3+2q+q2=（2+q）2，q=-
| 1 |
| 2 |
此时 c1=1，c2=
| 3 |
| 2 |
| 9 |
| 4 |
∴c1，c2，c3是一个公比为
| 3 |
| 2 |
如果m≥4，c1，c2，…，cm为等比数列，那么c1，c2，c3一定是等比数列．
由上所述，此时q=-
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
| 23 |
| 8 |
由于
| c4 |
| c3 |
| 3 |
| 2 |
综上所述，当且仅当m=3且q=-
| 1 |
| 2 |
②设x1，x2，x3和y1，y2，y3分别为第k+1列和第m+1列的前三项，1≤k＜m≤n-1，
则x1=1，x2=k+q，x3=(1+2+3+…+k)+kq+q2=
| k(k+1) |
| 2 |
若第k+1列的前三项x1，x2，x3是等比数列，则
由x1x3=
| x | 22 |
| k(k+1) |
| 2 |
| k2-k |
| 2 |
| 1-k |
| 2 |
同理，若第m+1列的前三项y1，y2，y3是等比数列，则q=
| 1-m |
| 2 |
当k≠m时，
| 1-k |
| 2 |
| 1-m |
| 2 |
所以，无论怎样的q，都不能同时找到两列数（除第1列外），使它们的前三项都成等比数列．
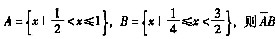表示为()。