问题
填空题
若函数f(x)=x2+ax-1在x∈[1,3]是单调递减函数,则实数a的取值范围是 ______.
答案
∵f(x)=x2+ax-1=(x+
)2-a 2
-1a2 4
∴其对称轴:x=-a 2
∵函数f(x)=x2+ax-1在x∈[1,3]是单调递减函数
∴x=-
≥3a 2
∴a≤-6
故答案为:a≤-6
若函数f(x)=x2+ax-1在x∈[1,3]是单调递减函数,则实数a的取值范围是 ______.
∵f(x)=x2+ax-1=(x+
)2-a 2
-1a2 4
∴其对称轴:x=-a 2
∵函数f(x)=x2+ax-1在x∈[1,3]是单调递减函数
∴x=-
≥3a 2
∴a≤-6
故答案为:a≤-6
某工程基础平面图如图1所示,现浇钢筋混凝土带形基础、独立基础的尺寸如图2所示。混凝土垫层强度等级为C15,混凝土基础强度等级为C20,按外购商品混凝土考虑。混凝土垫层支模板浇筑,工作面宽度300mm,槽坑底面用电动夯实机夯实,费用计入混凝土垫层和基础中。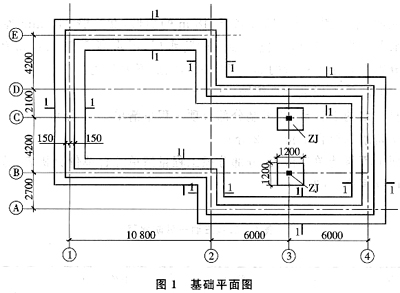
直接工程费单价表,如表3所示。
表3 直接工程费单价表
| 序号 | 项目名称 | 计量单位 | 费用组成(元) | ||||
| 人工费 | 材料费 | 机械使用费 | 单价 | ||||
| 1 | 带形基础组合钢模板 | m2 | 8.85 | 21.53 | 1.60 | 31.98 | |
| 2 | 独立基础组合钢模板 | m2 | 8.32 | 19.01 | 1.39 | 28.72 | |
| 3 | 垫层木模板 | m2 | 3.58 | 21.64 | 0.46 | 25.68 | |
基础定额表如表4所示。
表4 基础定额表
| 项目 | 基础槽底夯实 | 现浇混凝土基础垫层 | 现浇混凝土带形基础 | ||
| 名称 | 单位 | 单价(元) | 100m2 | 10m2 | 10m2 |
| 综合工日 | 工日 | 52.36 | 1.42 | 7.33 | 9.56 |
| 混凝土C15 | m3 | 252.40 | 10.15 | ||
| 混凝土C20 | m3 | 266.05 | 10.15 | ||
| 草袋子 | m2 | 2.25 | 1.36 | 2.52 | |
| 水 | m3 | 2.92 | 8.67 | 9.19 | |
| 电动打夯机 | 台班 | 31.54 | 0.56 | ||
| 混凝土振捣器 | 台班 | 23.51 | 0.61 | 0.77 | |
| 翻斗车 | 台班 | 154.80 | 0.62 | 0.78 | |
依据《建设工程工程量清单计价规范》计算原则,以人工费、材料费和机械使用费之和为基数,取管理费率5%、利润率4%;以分部分项工程量清单计价合计和模板及支架清单项目费之和为基数,取临时设施费率1.5%、环境保护费率0.8%、安全和文明施工费率1.8%。问题:
依据《建设工程工程量清单计价规范》(GB 50500—2008)的规定(有特殊注明除外)完成下列计算。
依据提供的基础定额数据,计算混凝土带形基础的分部分项工程量清单综合单价,填入“分部分项工程量清单综合单价分析表”,并列出计算过程。