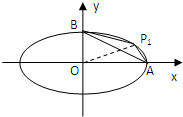
设P₁（4cosα，3sinα）（0＜α＜

π

2

），即点P₁在第一象限的椭圆上，考虑四边形P₁AOB面积S，

S=S_△OAP1+S_△OBP1=

1

2

×4（3sinα）+

1

2

×3（4cosα）=6（sinα+cosα）=6

2

sin（α+

π

4

），∴S_max=6

2

．

∵S_△OAB=

1

2

×4×3=6为定值，

∴S_△P1AB的最大值为6

2

-6．

∵6

2

-6＜3，

∴点P不可能在直线AB的上方，显然在直线AB的下方有两个点P，

故选B．