问题
填空题
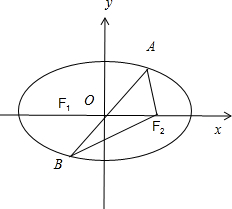
椭圆
|
答案
∵
+x2 45
=1中a=3y2 20
,b=25
,c=5,则的焦点分别为F1和(-5,0),F2(5,0)5
①当直线AB的斜率不存在时,直线AB的方程为x=0,此时AB=45
S△ABF2=
AB•5=1 2
×41 2
×5=105
不符合题意5
②可设直线AB的方程y=kx
联立方程
可得(4+9k2)x2=180y=kx
+x2 45
=1y2 20
∴xA=6
,yA=5 4+9k2 6
k5 4+9k2
∴AB=2AO=2×6 5+5k2 4+9k2
∴△ABF2的面积为S=2SAOF2=2×
×5×1 2
=206
k5 4+9k2
∴k=±4 3
∴直线AB的方程y=±
x4 3
故答案为y=±
x4 3