问题
解答题
已知二次函数f(x)=mx2-2x+m其中实数m为常数.
(1)求m的值,使函数f(x)的图象在x=0处的切线l与圆C:x2+y2-4x-2y=0也相切.
(2)当m>0时,求关于x的不等式f(x)≤0的解集M.
答案
(1)f(x)=mx2-2x+m,f(0)=m,f'(x)=2mx-2,f'(0)=-2.
则切线l的方程为y-m=-2x,即2x+y-m=0.
因为切线l与圆C:(x-2)2+(y-1)2=5相切,所以
=|5-m| 5
,即|m-5|=55
又m≠0.故m=10
(2)当m>0时,关于x的不等式f(x)≤0,即mx2-2x+m≤0,△=4-4m2
①当△>0,即0<m<1时,关于x的方程f(x)=0有两个不相等的实数解x=
,1± 1-m2 m
则M=[
,1- 1-m2 m
];1+ 1-m2 m
②当△=0,即m=1时,关于x的方程f(x)=0有两个相等的实数解x=1则M={1};
③当△<0,即m>1时,关于x的方程f(x)=0没有实数解,则M=∅.

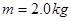 的滑块静止放在水平地面上的A点,受到一个大小为
的滑块静止放在水平地面上的A点,受到一个大小为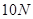 ,与水平方向成
,与水平方向成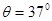 倾角斜向上恒力
倾角斜向上恒力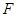 作用开始运动,当物体前进
作用开始运动,当物体前进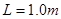 到达B点时撤去
到达B点时撤去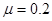 ,求BC间的距离x。(cos37o=0.8,sin37o=0.6,
,求BC间的距离x。(cos37o=0.8,sin37o=0.6,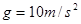 )
)