问题
解答题
已知函数f(x)=sin2x+acosx+
(1)当a=1时,求函数f(x)的最大值; (2)若x∈[0,
|
答案
化简可得f(x)=-cos2x+acosx+
a-5 8
,1 2
令t=cosx,所以f(x)=-t2+at+
a-5 8
,1 2
(1)当a=1时,f(x)=-t2+t+
=-(t-1 8
)2+1 2
,3 8
因为x∈R,所以t∈[-1,1],
关于t的二次函数开口向下,对称轴为t=
,1 2
故当t=
时,函数取最大值f(x)max=1 2
,…(8分)3 8
(2)因为x∈[0,
],所以t∈[0,1],π 2
由于函数对称轴为x=
,a 2
故当
≤0,即a≤0时,函数在x=0处,函数取最大值a 2
a-5 8
,1 2
当0<
<1,即0<a<2时,函数在x=a 2
处,函数取最大值a 2
+a2 4
a-5 8
,1 2
当
≥1,即a≥2时,函数在x=1处,函数取最大值a 2
-13a 8
,3 2
故f(x)max=
…(16分)
a-5 8
(a≤0)1 2
+a2 4
a-5 8
(0<a<2)1 2
a-13 8
(a≥2)3 2

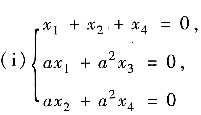 的解全是4元方程(ii)x1+x2+x3=0的解,
的解全是4元方程(ii)x1+x2+x3=0的解,