解；（1）由题意可设椭圆的标准方程为

x2

a2

+

y2

b2

=1，c为半焦距．

∵右顶点为D（2，0），左焦点为F(-

3

，0)，

∴a=2，c=

3

，b2=a2-c2=22-(

3

)2=1．

∴该椭圆的标准方程为

x2

4

+y2=1．

（2）设点P（x₀，y₀），线段PA的中点M（x，y）．

由中点坐标公式可得

x= x0+1 2 y= y0+ 1 2 2

，解得

x0=2x-1 y0=2y- 1 2

．（*）

∵点P是椭圆上的动点，∴

x 20

4

+

y

20

=1．

把（*）代入上式可得

(2x-1)2

4

+(2y-

1

2

)2=1，可化为(x-

1

2

)2+

(y- 1 4 )2

1 4

=1．

即线段PA的中点M的轨迹方程为一焦点在x轴上的椭圆(x-

1

2

)2+

(y- 1 4 )2

1 4

=1．

（3）①当直线BC的斜率不存在时，可得B（0，-1），C（0，1）．

∴|BC|=2，点A(1，

1

2

)到y轴的距离为1，∴S△ABC=

1

2

×2×1=1；

②当直线BC的斜率存在时，设直线BC的方程为y=kx，B（x₁，y₁），C（-x₁，-y₁）（x₁＜0）．

联立

y=kx x2+4y2=4

，化为（1+4k²）x²=4．解得x1=-

2

1+4k2

，

∴y1=-

2k

1+4k2

．

∴|BC|=

4 x 21 +4 y 21

=2

(- 2 1+4k2 )2+(- 2k 1+4k2 )2

=

4 1+k2

1+4k2

．

又点A到直线BC的距离d=

|k- 1 2 |

1+k2

．

∴S△ABC=

1

2

|BC|×d=

1

2

×

4 1+k2

1+4k2

|k- 1 2 |

1+k2

=

|2k-1|

1+4k2

，

∴

S

2△ABC

=

(2k-1)2

1+4k2

=1-

4k

1+4k2

，

令f（k）=

4k

1+4k2

，则f′(k)=

-16(k+ 1 2 )(k- 1 2 )

(1+4k2)2

．

令f′（k）=0，解得k=±

1

2

．列表如下：

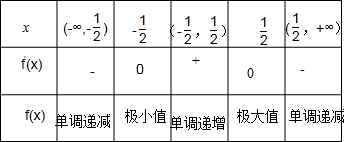
又由表格可知：当k=-

1

2

时，函数f（x）取得极小值，即

S

2△ABC

取得最大值2，即S△ABC=

2

．

而当x→+∞时，f（x）→0，

S

2△ABC

→1．

综上可得：当k=-

1

2

时，△ABC的面积取得最大值

2

，即S△ABC=

2

．