问题
解答题
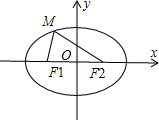
已知椭圆C的中心为坐标原点，离心率为
（1）求椭圆C的标准方程； （2）若直线m过F1点，且与椭圆相交于A、B两点，|AF2|+|BF2|=
|
答案
（1）∵椭圆的离心率为
，|MF1|+|MF2|=22 2 2
∴
=c a 2 2 2a=2 2
∴a=
，c=12
∴b=1
∴椭圆C的标准方程为
+y2=1；x2 2
（2）由（1）知，F1（-1，0），设直线m的方程为x=my-1
代入椭圆方程可得（m2+2）y2-2my-1=0
设A（x1，y1），B（x2，y2），则y1+y2=
，y1y2=2m m2+2 -1 m2+2
∴|AB|=
|y1-y2|=1+m2
•1+m2 (
)2-4•2m m2+2 -1 m2+2
∵|AF2|+|BF2|=8 2 3
∴|AB|=4
-2
=8 2 3 4 2 3
∴
•1+m2
=(
)2-4•2m m2+2 -1 m2+2 4 2 3
∴m=±1
∴直线m的方程为y=±（x+1）
轴进入教室的风道底标高应为 ( )。