问题
解答题
已知点A(8,0)及在第一象限的动点P(x,y),且x+y=10,设△OPA的面积为S.
(1)求S关于x的函数关系式,并写出自变量x的取值范围;
(2)求S=12时P点坐标;
(3)在(2)的基础上,设点Q为y轴上一动点,当PQ+AQ的值最小时,求Q点坐标.
答案
(1)∵x+y=10
∴y=10-x,
∴s=8(10-x)÷2=40-4x,
∵40-4x>0,
∴x<10,
∴0<x<10,
(2)∵s=12,
∴12=40-4x,
x=7
∴y=10-7=3,
∴s=12时,P点坐标(7,3),
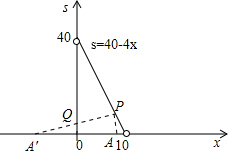
(3)画出函数S的图形如图所示.
作出A的对称点A′,连接PA′,此时PA′与y轴交于点Q,此时PQ+AQ的值最小,
∵A点坐标为(8,0),
∴A′(-8,0),
∴将(-8,0),(7,3)代入y=kx+b,
∴
,0=-8k+b 3=7k+b
解得:
,k= 1 5 b= 8 5
∴y=
x+1 5
,8 5
∴x=0时,y=
,8 5
当PQ+AQ的值最小时,Q点坐标为:(0,
).8 5