问题
填空题
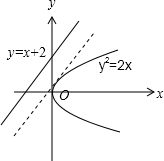
已知点P为抛物线y2=2x上的动点,则点P到直线y=x+2的距离的最小值为______.
答案
如图,
设与直线y=x+2平行的直线方程为y=x+m.
联立
,得x2+(2m-2)x+m2=0.y=x+m y2=2x
由△=(2m-2)2-4m2=0,得m=
.1 2
所以与直线y=x+2平行且与抛物线y2=2x相切的直线方程为y=x+
.1 2
由两平行线间的距离公式得:d=
=|2-
|1 2 12+(-1)2
.3 2 4
所以点P到直线y=x+2的距离的最小值为
.3 2 4
故答案为
.3 2 4