问题
选择题
若动圆过定点A(-3,0)且和定圆(x-3)2+y2=4外切,则动圆圆心P的轨迹为( )
A.双曲线
B.椭圆
C.抛物线
D.双曲线一支
答案
设动圆的半径为R,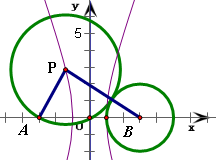
∵动圆圆心为P,点A在动圆上,∴|PA|=R
又∵定圆(x-3)2+y2=4的圆心为B(3,0),半径为2,
定圆与动圆P相外切
∴圆心距|PB|=R+2
由此可得|PB|-|PA|=(R+2)-R=2(常数),
∴点P的轨迹是以A、B为焦点的双曲线的左支
故选:D
