问题
选择题
过抛物线y2=2px(p>0)的焦点F作直线与抛物线交于A、B两点,以AB为直径的圆与抛物线的准线的位置关系是( )
A.相交
B.相切
C.相离
D.与p的取值相关
答案
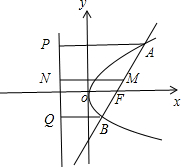
取AB的中点M,分别过A、B、M作准线的垂线AP、BQ、MN,垂足分别为P、Q、N,如图所示:
由抛物线的定义可知,|AP|=|AF|,|BQ|=|BF|,
在直角梯形APQB中,|MN|=
(|AP|+|BQ|)=1 2
(|AF|+|BF|)=1 2
|AB|,1 2
故圆心M到准线的距离等于半径,
∴以AB为直径的圆与抛物线的准线相切,
故选B.