问题
问答题
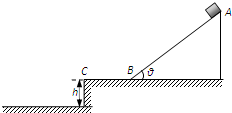
如图所示,光滑斜面AB与光滑水平面BC平滑连接.斜面AB长度L=3.0m,倾角θ=37°.一小物块在A点由静止释放,先后沿斜面AB和水平面BC运动,接着从点C水平抛出,最后落在水平地面上.已知水平面BC与地面间的高度差h=0.80m.取重力加速度g=10m/s2,sin37°=0.60,cos37°=0.80.不计空气阻力.求
(1)小物块沿斜面AB下滑过程中加速度的大小a;
(2)小物块到达斜面底端B时速度的大小v;
(3)小物块从C点水平抛出到落在地面上,在水平方向上位移的大小x.
答案
(1)对物体受力分析,受重力和支持力,根据牛顿第二定律,有
mgsinθ=ma
解得:a=gsinθ=6.0m/s2
(2)根据机械能守恒定律 mgsinθL=
mv21 2
解得:v=
=6.0m/s2gLsinθ
(3)物体做平抛运动,水平方向上分运动为匀速直线运动 x=vt ①
竖直方向上分运动为自由落体运动 h=
gt2 ②1 2
上述①、②两式联立,解得:x=v
=2.4m2h g
答:(1)小物块沿斜面AB下滑过程中加速度的大小a为6.0m/s2;
(2)小物块到达斜面底端B时速度的大小v为6.0m/s;
(3)小物块从C点水平抛出到落在地面上,在水平方向上位移的大小x为2.4m.
