问题
解答题
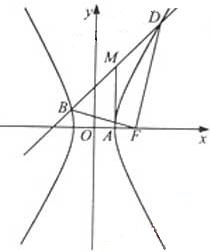
己知斜率为1的直线l与双曲线C:
(Ⅰ)求C的离心率; (Ⅱ)设C的右顶点为A,右焦点为F,|DF|•|BF|=17,证明:过A、B、D三点的圆与x轴相切. |
答案
(Ⅰ)由题设知,l的方程为:y=x+2,代入C的方程,并化简,
得(b2-a2)x2-4a2x-a2b2-4a2=0,
设B(x1,y1),D(x2,y2),则x1+x2=
,x1x2=-4a2 b2-a2
,①4a2+a2b2 b2-a2
由M(1,3)为BD的中点知
=1.x1+x2 2
故
×1 2
=1,即b2=3a2,②4a2 b2-a2
故c=
=2a,a2+b2
∴C的离心率e=
=2.c a
(Ⅱ)由①②知,C的方程为:3x2-y2=3a2,A(a,0),F(2a,0),
x1+x2=2,x1x2=-
.4+3a2 2
故不妨设x1≤-a,x2≥a,
|BF|=
=a-2x1,|FD|=(x1-2a)2+y12
=2x2-a,(x2-2a)2+y22
|BF|•|FD|=(a-2x1)(2x2-a)=-4x1x2+2a(x1+x2)-a2=5a2+4a+8.
又|BF|•|FD|=17,故5a2+4a+8=17.
解得a=1,或a=-
(舍去),9 5
故|BD|=
|x1-x2|=2 2
=6,(x1+x2)2-4x1x2
连接MA,则由A(1,0),M(1,3)知|MA|=3,
从而MA=MB=MD,且MA⊥x轴,
因此以M为圆心,MA为半径的圆经过A、B、D三点,且在点A处与x轴相切,
所以过A、B、D三点的圆与x轴相切.