问题
填空题
过椭圆左焦点F,倾斜角为
|
答案
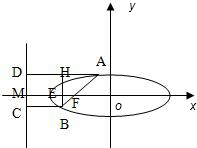
设准线与x轴交点为M,过A、B作准线的垂线,垂足分别为D、C,过B作BH⊥AD,垂足为H,交x轴于E.
设|AB|=3t,因为|FA|=2|FB|,则|BF|=t,|AF|=2t,
因为AB倾斜角为60°,所以∠ABH=30°,则|AH|=
|AB|=1 2
t,3 2
根据椭圆第二定义,可得|AH|=|AD|-|BC|=
-2t e
=t e
,t e
∴
t=3 2 t e
∴e=
,2 3
故答案为:
.2 3