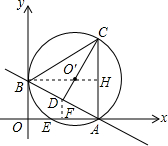
问题
解答题
已知:直线y=-
(1)求C点坐标. (2)求过点C与AB中点D的一次函数的解析式. (3)求过E、O′、A三点的二次函数的解析式. |
答案
(1)∵直线y=-
x+1与x轴、y轴分别交于A、B两点,3 3
∴A(
,0),B(0,1),3
在Rt△ABO中,
∵AB=
=2,OA2+OB2
∴tan∠BAO=
=1 3
,3 3
∴∠BAO=30°
又∵△ABC是等边三角形
∴AC=AB=2,∠BAC=60°,
∴∠OAC=90°
∴CA∥OB,
∴C点坐标为(
,2);3
(2)∵D是AB的中点,过D作DF∥OB,交OA于F,
则DF=
OB=1 2
,OF=1 2
OA=1 2 3 2
∴D点坐标为(
,3 2
),1 2
设过C、D两点的一次函数解析式为y=kx+b(k≠0),
则
,解得
k+b=03
k+b=3 2 1 2
,k= 3 b=-1
∴所求一次函数的解析式为y=
x-1;3
(3)过点B作BH⊥AC于点H,
∵△ABC是等边△,
∴BH是AC的垂直平分线,
∴BF过点O′,
∵B(0,1),
∴当y=1时,x=2 3 3
∴O′(
,1),2 3 3
∵CA∥BO,BH⊥AC,
∴BH⊥OB,且过⊙O′半径的外端,
∴OB是⊙O′的切线,
∴OB2=OE•OA,即1=OE•
,解得OE=3
,3 3
∴E(
,0),3 3
设过E、O′、A三点的抛物线为y=ax2+bx+c,将三点坐标代入得
3a+
b+c=03
a+4 3
+c=12
b3 3
a+b+c=01 3
解得a=-3 b=4 3 c=-3
∴所求二次函数的解析式为y=-3x2+4
x-3.3