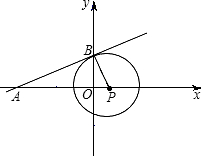
问题
解答题
直线l的解析式y=
(1)求点P的坐标及⊙P的半径R; (2)若⊙P以每秒
(3)在(2)中,设⊙P被直线l截得的弦长为a,问是否存在t的值,使a最大?若存在,求出t的值. |
答案
(1)如图,由于直线l:y=
x+8与x轴、y轴分别交于A、B两点,所以A、B两点的坐标可以求出,线段OA、OB的长度也可以求出,又OB⊥AP,AB切⊙P于B点,可以得到△ABO∽△BPO,然后根据相似三角形的对应边成比例就可以求出OP,BP,也就求出了题目的结论;3 4
求得P点坐标(6,0),半径PB=10.
(2)若⊙P以每秒
个单位沿x轴向左运动,同时⊙P的半径以每秒10 3
个单位变小,3 2
设⊙P的运动时间为t秒,且⊙P始终与直线l有交点,试求t的取值范围;
R≥点P到直线L的距离,则⊙P始终与直线l有交点.
P[(6-
t),0],R=10-10 3
t,L:3x-4y+32=03 2
点P到直线L的距离H=|10-2t|
10-
t≥|10-2t|3 2
10-
t≥10-2t≥-(10-3 2
t)3 2
解得:0≤t≤
;40 7
(3)在(2)中,设⊙P被直线l截得的弦长为a,问是否存在t的值,使a最大?若存在,求出t的值
一定存在t的值,使a最大
(
)2=R2-H2=(10-a 2
t)2-(10-2t)2=(-3 2
)•(t-32 9
)2+5015 4
则a2=-7t2+40t,
t=
=40 14
时,a2最大=20 7
,a最大=400 7
.20 7 7