问题
解答题
已知:在平面直角坐标系中,点A(1,0),点B(4,0),点C在y轴正半轴上,且OB=2OC.
(1)试确定直线BC的解析式;
(2)在平面内确定点M,使得以点M、A、B、C为顶点的四边形是平行四边形,请直接写出点M的坐标.
答案
(1)∵B(4,0),∴OB=4,
又∵OB=2OC,C在y轴正半轴上,
∴C(0,2).
设直线BC的解析式为y=kx+b(k≠0).
∵过点B(4,0),C(0,2),
∴
,4k+b=0 b=2
解得
,k=- 1 2 b=2
∴直线BC的解析式为y=-
x+2.1 2
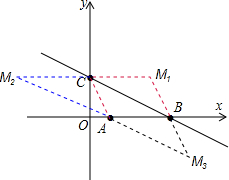
(2)如图,①当BC为对角线时,易求M1(3,2);
②当AC为对角线时,CM∥AB,且CM=AB.所以M2(-3,2);
③当AB为对角线时,AC∥BM,且AC=BM.则|My|=OC=2,|Mx|=OB+OA=5,所以M3(5,-2).
综上所述,符合条件的点M的坐标是M1(3,2),M2(-3,2),M3(5,-2).