∵直线y=-

3

3

x+

3

交x轴于点A，交y轴于点C，

∴A（3，0），B（0，

3

），

∵OC=

3

，OA=3，

∴tan∠CAO=

OC

OA

=

3

3

，

∴∠CAO=30°，

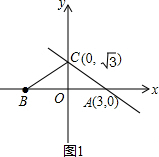
当点B在x轴上，且BC=AB时（如图1），

∵OC⊥x轴，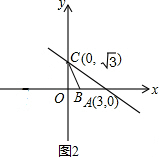

∴点O是AB的中点，

∵点A（3，0），

∴B（-3，0）；

当BC=AB时（如图2），设B（a，0），则a²+（

3

）²=（3-a）²，解得a=1，

∴B（1，0）；

当点B在y轴上时（如图3）：

∵∠CAO=30°，∠AOC=90°，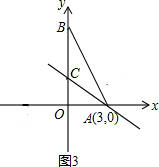

∴∠ACO=60°，

∴∠BCA=180°-∠ACO=180°-60°=120°，

若BC=AC，则∠BAC=

180°-∠ABC

2

=

180°-120°

2

=30°，

∴此种情况符合题意，

设点B（0，y），则（y-

3

）²=3²+（

3

）²，解得y=3

3

，

∴B（0，3

3

）．

综上所述，符合条件的B点坐标为：（-3，0）；（0，3

3

）；（1，0）．

故答案为：（-3，0）；（0，3

3

）；（1，0）．