问题
解答题
已知关于x的方程kx2﹣2（k+1）x+k﹣1=0有两个不相等的实数根．
（1）求k的取值范围；
（2）是否存在实数k，使此方程的两个实数根的倒数和等于0？若存在，求出k的值；若不存在，说明理由．
答案
解：（1）∵方程有两个不相等的实数根，
∴△=[﹣2（k+1）]2﹣4k（k﹣1）=12k+4＞0，且k≠0，
解得k＞﹣
，且k≠0，
即k的取值范围是k＞﹣
，且k≠0；
（2）假设存在实数k，使得方程的两个实数根x1，x2的倒数和为0，则x1，x2不为0，
且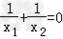
，即
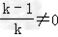，且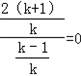
，
解得k=﹣1，而k=﹣1与方程有两个不相等实根的条件k＞﹣1，且k≠0矛盾，
故使方程的两个实数根的倒数和为0的实数k不存在．