解：（1）将原方程整理为：x²﹣（2k+1）x+k²﹣2=0，

∵原方程有两个实数根，

∴△=[﹣（2k+1）]²﹣4×1×（k²﹣2）=4k+9≥0，

解得：k≥；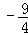

（2）∵x₁，x₂为x²﹣（2k+1）x+k²﹣2=0的两根，

∴y=x₁+x₂=2k+1，且k≥，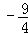

因而y随k的增大而增大，

故当k=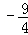时，y有最小值．

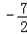故答案为：k≥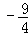，﹣．