问题
解答题
已知关于x的方程2x2﹣(4k+1)x+2k2﹣1=0,问当k取什么值时,
(1)方程有两个不相等的实数根;
(2)方程有两个相等的实数根;
(3)方程没有实数根.
答案
解:∵a=2,b=﹣(4k+1),c=2k2﹣1,
∴△=b2﹣4ac=[﹣(4k+1)]2﹣4×2×(2k2﹣1)=8k+9,
(1)∵方程有两个不相等的实数根,
∴△>0,
即8k+9>0,
解得k> .
.
(2)∵方程有两个相等的实数根,
∴△=0,
即8k+9=0,
解得k= .
.
(3)∵方程没有实数根,
∴△<0,
即8k+9<0,
解得k<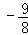 .
.

 等消防标志的是
等消防标志的是