问题
解答题
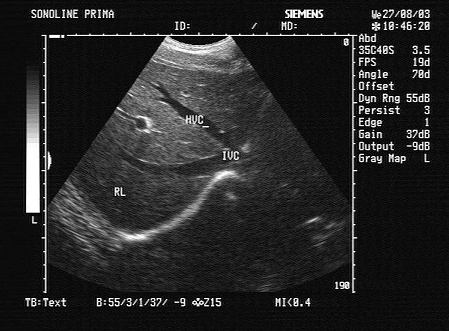
无论p取何值,关于x的方程(x﹣3)(x﹣2)﹣p2=0①总有两个不相等的实数根吗?给出答案并说明理由.再求出当方程①有一个解为x=1时,p的值是多少?
答案
解:无论p取何值,关于x的方程(x﹣3)(x﹣2)﹣p2=0①总有两个不相等的实数根,
∵(x﹣3)(x﹣2)﹣p2=0,
∴x2﹣5x+6﹣p2=0,
∴△=25﹣4(6﹣p2)=4p2+1,
而4p2≥0,
∴△>0,
∴无论p取何值,关于x的方程(x﹣3)(x﹣2)﹣p2=0①总有两个不相等的实数根;
当方程①有一个解为x=1时,
1﹣5+6﹣p2=0,
∴p2=2,
∴p=±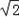 .
.