问题
解答题
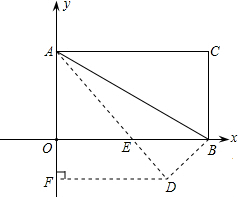
已知:把矩形AOBC放入直角坐标系xOy中,使OB、OA分别落在x轴、y轴上,点A的坐标为(0,2
(1)求D点坐标; (2)求经过点A、D的直线的解析式. |
答案
根据题意,可分以下两种情况:
第一种情况矩形在第一象限,如图.
(1)OA=2
,∠AOB=90°,∠OAB=60°,3
∴OB=OA•tan60°=2
•3
=6.3
又Rt△ACB≌Rt△ADB,
∴AC=AD=OB=6.
过点D作y轴的垂线,垂足为F,
∠OAB=60°,
∴∠BAC=∠BAD=∠DAF=30°.
∴DF=
AD=3.1 2
AF=AD•cos30°=6×
=33 2
,3
∴OF=AF-OA=3
-23
=3
.3
∴点D的坐标为(3,-
).3
(2分)
(2)设经过点A(0,2
)、D(3,-3
)的直线的解析式为y=kx+b,3
,b=2 3 3k+b=- 3
解得
.b=2 3 k=- 3
∴经过点A、D的直线的解析式为y=-
x+23
. (4分)3
第二种情况矩形在第二象限,(图略)
(1)由第一种情况,根据对称性得,点D的坐标为(-3,-
).(5分)3
(2)设经过点A(0,2
)、D(3,-3
)的直线的解析式为y=kx+b,3
,b=2 3 -3k+b=- 3
解得
.k= 3 b=2 3
∴经过点A、D的直线的解析式为y=
x+23
. (7分)3