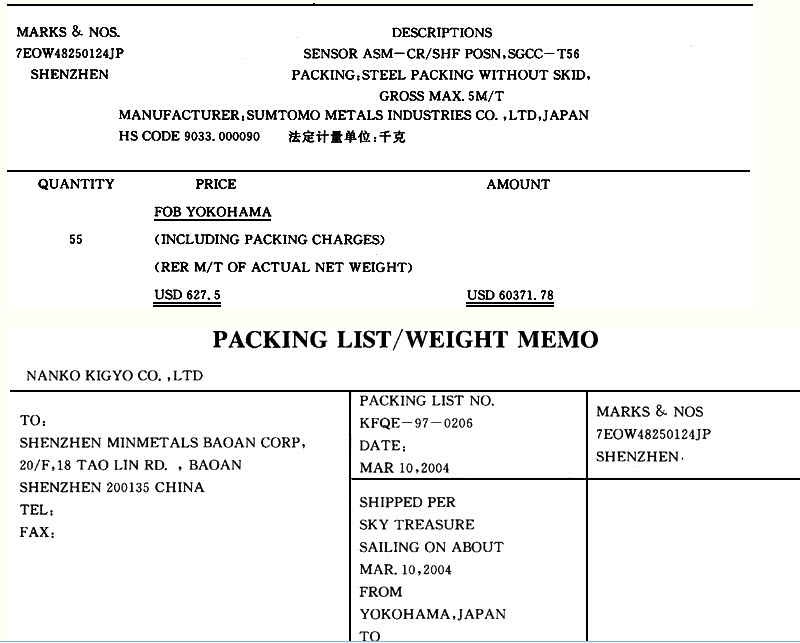
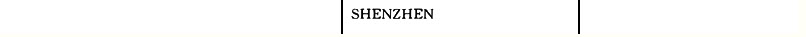问题
解答题
已知:等比数列{an}的首项为a1,公比为q.
(1)写出数列{an}的前n项和Sn的公式;
(2)给出(1)中的公式的证明.
答案
(1)Sn=
;na1,q=1
,q≠1a1(1-qn) 1-q
(2)由等比数列及其前n项和的定义知:Sn=a1+a2+…+an=a1+a1q+a1q2+…+a1qn-2+a1qn-1①
当q=1时,Sn=na1;
当q≠1时,把①式两边同乘q,得qSn=a1q+a1q2+a1q3+…+a1qn-1+a1qn②
由①-②,得(1-q)Sn=a1-a1qn=a1(1-qn),∴Sn=
.a1(1-qn) 1-q
综上:当q=1时,Sn=na1;当q≠1时,Sn=
.a1(1-qn) 1-q

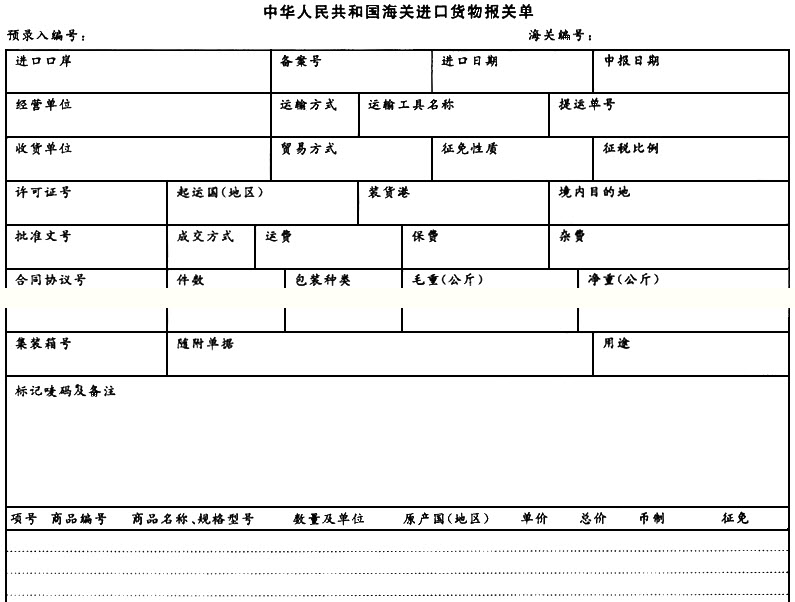
 (二)
(二)