答案：C

本题考查了垂径定理：平分弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了勾股定理．连结OC，根据垂径定理得到CE=4，再根据勾股定理计算出OE=3，分类讨论：当点E在半径OB上时，BE=OB﹣OE；当点E在半径OA上时，BE=OB+OE，然后把CE、OE的值代入计算即可．

解：如图，连结OC，

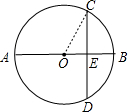
∵直径AB⊥CD，

∴CE=DE=CD=×8=4，

在Rt△OCE中，OC=AB=5，

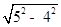∴OE==3，

当点E在半径OB上时，BE=OB﹣OE=5﹣3=2，

当点E在半径OA上时，BE=OB+OE=5+3=8，

∴BE的长为2或8．

故选C．