阅读下文,回答问题。
斗士的风格
谢柏梁
窦娥敢于在法场上骂地恨天:
没来由犯王法,不提防遭刑宪,叫声屈动地惊天。顷刻间游魂先赴森罗殿,怎不将天地也生埋怨。
有日月朝暮悬,有鬼神掌着生死权。天地也!只合把清浊分辨,可怎生糊突了盗跖、颜渊?为善的受贫穷更命短,造恶的享富贵又寿延。天地也!做得个怕硬欺软,却原来也这般顺水推船!
这是对天地鬼神及当时社会秩序的怀疑、指责和否定。为什么天地分不清好人恶人?为什么神鬼也欺软怕硬?为什么日月也顺水推舟、落井下石?该不该取消你们这些日月、天地和鬼神的资格?此时的窦娥,哪里是一位含冤负屈、悲苦无告的弱女子,她分明是一位评点江山、指挥天地、浩然正气布满乾坤的“复仇女神”。
她要求半星热血不染尘,殷红的鲜血都只在旗枪素练上绽开红花;她命令六月天下大雪,那洁白的瑞雪便纷纷扬扬,包裹了她洁白的身体;她要楚州地面亢旱三年,以证明她的旷世奇冤,楚州大地果然就乖乖地裂开了干渴的大口。应该说,窦娥对天地的怀疑和指责,更多的是体现着关汉卿奇才大略却又悲苦郁闷、借题发挥的愤怒哲学,这和屈原《离骚》《天问》的精神是相通的。
关汉卿又借窦娥之口,否定了作为国家机器主要部分的衙门:“这的是衙门从古向南开,就中无个不冤哉!痛杀我娇姿弱体闭泉台,早三年以外,则落的悠悠流恨似长淮!”
窦娥之冤,并不是偶然的个别的现象,而只是历史冤河的一星浪花。窦娥的愤怒不仅是对元代统治者的愤怒,还是对古往今来一切黑暗无道的封建统治的控诉。
这就 使得关汉卿的深刻思想触及了剥削社会的本质部分。而且关汉卿的伟大之处不仅在于提出问题,让观众们从精神上去评判和平反冤狱,而且还让剧中人自己为自己裁判,自己为自己雪冤。过去常有人认为《窦娥冤》中最后出现的“清官断案”是削弱了作品的战斗性,但其实窦娥只不过是假“清官”之手,说出自己要说的话,做出自己要做的事,她是破冤案的幕后指挥,又是幕前大打出手的中心人物。她支配着包括父亲在内的全部出场人,也支配着全体观众的心理。没有窦天章,也会有张天章、李天章来实现她复仇的愿望。在这里,关汉卿的意志、窦娥的意志与人民的意志以及窦天章们为实现这个意志而行动的过程都是一致的。 (有删改)
使得关汉卿的深刻思想触及了剥削社会的本质部分。而且关汉卿的伟大之处不仅在于提出问题,让观众们从精神上去评判和平反冤狱,而且还让剧中人自己为自己裁判,自己为自己雪冤。过去常有人认为《窦娥冤》中最后出现的“清官断案”是削弱了作品的战斗性,但其实窦娥只不过是假“清官”之手,说出自己要说的话,做出自己要做的事,她是破冤案的幕后指挥,又是幕前大打出手的中心人物。她支配着包括父亲在内的全部出场人,也支配着全体观众的心理。没有窦天章,也会有张天章、李天章来实现她复仇的愿望。在这里,关汉卿的意志、窦娥的意志与人民的意志以及窦天章们为实现这个意志而行动的过程都是一致的。 (有删改)
小题1:为什么说窦娥是一位“复仇女神”?(3分)
_________________________________ ______________________________
______________________________ ______________________________________________________________________。
______________________________________________________________________。
小题2:“而只是历史冤河的一星浪花”在文中的含义是什么?(4分)
_____________________________________________________________________________________________________________________________________。
小题3:“剧中人自己为自己裁判,自己为自己雪冤”的意思是什么?(4分)
_____________________________________________________________________________________________________________________________________。
小题4:下面对文章有关内容的评析,不恰当的两项是(5分)( )
A.窦娥对天地鬼神以及人间的现有制度不但表现出清醒的认识,而且作出了实际的抗争。
B.“诗言志”,同样,戏剧也能反映作者的内在思想,关汉卿借窦娥鞭挞了他所憎恨的社会。
C.司马迁说屈原忧愁幽思而作《离骚》,关汉卿也是发自内心悲苦郁闷之情而著《窦娥冤》。
D.“支配着观众的心理”意即窦娥的形象以及她的性格发展在观众的心理上产 生了极大共鸣。E.作者高度评价了关汉卿所塑造的窦娥形象,赞其无私无畏的批判精神,具有鲜明的追求个性解放的精神。
生了极大共鸣。E.作者高度评价了关汉卿所塑造的窦娥形象,赞其无私无畏的批判精神,具有鲜明的追求个性解放的精神。
 ,
, ,
, ,
,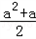 =
= (a+
(a+ )2﹣
)2﹣ ,
, 时,
时,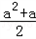 有最小值﹣
有最小值﹣ ,
, 。
。
 使得关汉卿的深刻思想触及了剥削社会的本质部分。而且关汉卿的伟大之处不仅在于提出问题,让观众们从精神上去评判和平反冤狱,而且还让剧中人自己为自己裁判,自己为自己雪冤。过去常有人认为《窦娥冤》中最后出现的“清官断案”是削弱了作品的战斗性,但其实窦娥只不过是假“清官”之手,说出自己要说的话,做出自己要做的事,她是破冤案的幕后指挥,又是幕前大打出手的中心人物。她支配着包括父亲在内的全部出场人,也支配着全体观众的心理。没有窦天章,也会有张天章、李天章来实现她复仇的愿望。在这里,关汉卿的意志、窦娥的意志与人民的意志以及窦天章们为实现这个意志而行动的过程都是一致的。 (有删改)
使得关汉卿的深刻思想触及了剥削社会的本质部分。而且关汉卿的伟大之处不仅在于提出问题,让观众们从精神上去评判和平反冤狱,而且还让剧中人自己为自己裁判,自己为自己雪冤。过去常有人认为《窦娥冤》中最后出现的“清官断案”是削弱了作品的战斗性,但其实窦娥只不过是假“清官”之手,说出自己要说的话,做出自己要做的事,她是破冤案的幕后指挥,又是幕前大打出手的中心人物。她支配着包括父亲在内的全部出场人,也支配着全体观众的心理。没有窦天章,也会有张天章、李天章来实现她复仇的愿望。在这里,关汉卿的意志、窦娥的意志与人民的意志以及窦天章们为实现这个意志而行动的过程都是一致的。 (有删改) ______________________________
______________________________ 生了极大共鸣。E.作者高度评价了关汉卿所塑造的窦娥形象,赞其无私无畏的批判精神,具有鲜明的追求个性解放的精神。
生了极大共鸣。E.作者高度评价了关汉卿所塑造的窦娥形象,赞其无私无畏的批判精神,具有鲜明的追求个性解放的精神。