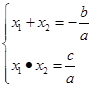问题
解答题
（本题满分12分）
在平面直角坐标系xOy中，抛物线C的顶点在原点，经过点A(2,2)，其焦点F在x轴上．
(1)求抛物线C的标准方程；
(2)设直线l是抛物线的准线，求证：以AB为直径的圆与准线l相切．
答案
(1) y2＝2x (2)关键证明AB的中点到准线的距离等于AB的一半。
题目分析：解：(1)设抛物线y2＝2px(p>0)，将点(2,2)代入得p＝1.
∴y2＝2x为所求抛物线的方程．
(2)证明：设lAB的方程为：x＝ty＋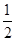
，代入y2＝2x得：y2－2ty－1＝0，设AB的中点为M(x0，y0)，则y0＝t，x0＝
.
∴点M到准线l的距离d＝x0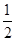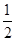＋＝＋＝1＋t2.又AB＝2x0＋p＝1＋2t2＋1＝2＋2t2，∴d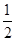＝AB，故以AB为直径的圆与准线l相切．
点评：求抛物线的方程，前提是设抛物线的方程，而设置抛物线可结合焦点，像本题通过画图，知道抛物线的焦点在x轴的正半轴上，因而可令抛物线的方程为y2＝2px(p>0)（式子中的x 对应x轴，2px前面是正的对应正半轴）。第二题涉及直线与抛物线这两种曲线，当两者相交时，常常在联立方程组后，用到根与系数的关系式：