问题
解答题
已知抛物线y=ax2(a≠0)的准线方程为y=-1,
(Ⅰ)求抛物线的方程;
(Ⅱ)设F是抛物线的焦点,直线l:y=kx+b(k≠0)与抛物线交于A,B两点,记直线AF,BF的斜率之和为m,求常数m,使得对于任意的实数k(k≠0),直线l恒过定点,并求出该定点的坐标。
答案
解:(Ⅰ)∵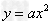 ,
,
∴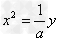 ,
,
∴抛物线C的准线方程为: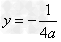 ,
,
∴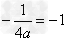 ,解得
,解得 ,
,
∴抛物线C的方程是 。
。
(Ⅱ)F(0,1),
设A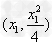 ,B
,B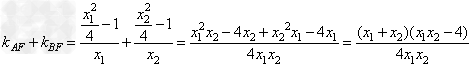 ,
,
由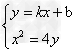 ,得
,得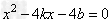 ,
,
∴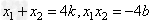 ,
, ,
,
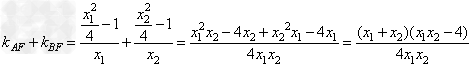
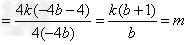 ,
,
∴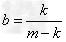 ,
,
∴直线 ,
,
令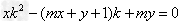 对任意的k(k≠0)恒成立,
对任意的k(k≠0)恒成立,
则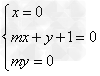 ,解得
,解得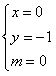 ,
,
所以,m=0,直线l过定点(0,-1)。
