问题
填空题
与直线x+2y+3=0垂直，且与抛物线y = x2 相切的直线方程是 ．
答案
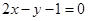
题目分析：设所求直线为2x-y+c=0,∵直线2x-y+c=0与抛物线y = x2 相切，联立方程消y得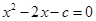
，∴
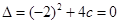，∴c=-1，∴所求直线为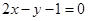
点评：判别式法是解决直线与圆锥曲线位置关系的常用方法，属基础题
搜题请搜索小程序“爱下问搜题”
与直线x+2y+3=0垂直，且与抛物线y = x2 相切的直线方程是 ．
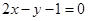
题目分析：设所求直线为2x-y+c=0,∵直线2x-y+c=0与抛物线y = x2 相切，联立方程消y得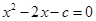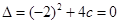，∴，∴c=-1，∴所求直线为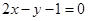
点评：判别式法是解决直线与圆锥曲线位置关系的常用方法，属基础题