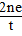问题
解答题
已知函数f(x)=x2+(2k-3)x+k2-7的零点分别是-1和-2
(1)求k的值;
(2)若x∈[-2,2],则f(x)<m恒成立,求m的取值范围.
答案
(1)∵函数f(x)=x2+(2k-3)x+k2-7的零点分别是-1和-2,∴-1和-2是x2+(2k-3)x+k2-7=0的根,
∴-1+(-2)=3-2k,解得 k=3.
(2)由(1)可得 函数f(x)=x2+3x+2,由于x∈[-2,2]时,f(x)<m恒成立,
故m大于函数f(x)=x2+3x+2 在[-2,2]上的最大值.
再由函数f(x)=x2+3x+2 在[-2,2]上的最大值为f(-
)=-3 2
,故m>-1 4
,1 4
即m的取值范围为(-
,+∞).1 4