问题
解答题
设A（x1，y1），B（x2，y2）两点在抛物线y=2x2上，l是AB的垂直平分线，
（Ⅰ）当且仅当x1+x2取何值时，直线l经过抛物线的焦点F？证明你的结论；
（Ⅱ）当x1=1，x2=﹣3时，求直线l的方程．
答案
解：（Ⅰ）∵抛物线y=2x2，即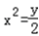 
，
∴
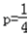， ∴焦点为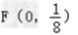
（1）直线l的斜率不存在时，显然有x1+x2=0
（2）直线l的斜率存在时，设为k，截距为b 即直线l：y=kx+b
由已知得：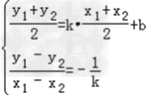
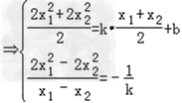
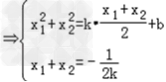
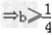
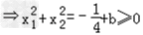
即l的斜率存在时，不可能经过焦点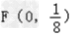
所以当且仅当x1+x2=0时，直线l经过抛物线的焦点F
（Ⅱ）当x1=1，x2=﹣3时，直线l的斜率显然存在，设为l：y=kx+b
则由（Ⅰ）得：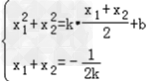
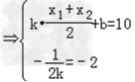
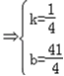
所以直线l的方程为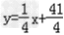
，即x﹣4y+41=0