问题
解答题
已知函数y=kx与y=x2+2(x≥0)的图象相交于A(x1,y1),B(x2,y2),l1,l2分别是y=x2+2(x≥0)的图象在A,B两点的切线,M,N分别是l1,l2与x轴的交点。
(1)求k的取值范围;
(2)设t为点M的横坐标,当x1<x2时,写出t以x1为自变量的函数式,并求其定义域和值域;
(3)试比较|OM|与|ON|的大小,并说明理由(O是坐标原点)。
答案
解:(1)由方程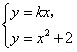 消y得
消y得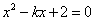 ①
①
依题意,该方程有两个正实根
故 解得
解得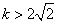 。
。
(2)由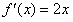 ,求得
,求得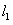 切线的方程为
切线的方程为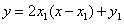 ,
,
由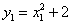 ,并令
,并令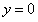 ,得
,得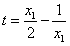 ,
,
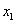 ,
,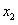 是方程①的两实根,且
是方程①的两实根,且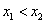 ,
,
故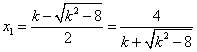 ,
,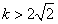 ,
,
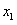 是关于k的减函数,所以
是关于k的减函数,所以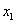 的取值范围是
的取值范围是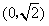
t是关于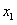 的增函数,定义域为
的增函数,定义域为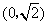 ,所以值域为
,所以值域为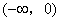 ,
,
(3)当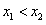 时,由(2)可知
时,由(2)可知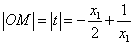
类似可得 ,
,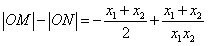
由①可知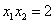
从而
当 时,有相同的结果
时,有相同的结果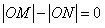
所以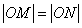 。
。
