问题
解答题
若A、B是抛物线y2=4x上的不同两点,弦AB(不平行于y轴)的垂直平分线与x轴相交于点P,则称弦AB是点P的一条“相关弦”。已知当x>2时,点P(x,0)存在无穷多条“相关弦”。给定x0>2。
(1)证明:点P(x0,0)的所有“相关弦”中的中点的横坐标相同;
(2)试问:点P(x0,0)的“相关弦”的弦长中是否存在最大值?若存在,求其最大值(用x0表示):若不存在,请说明理由。
答案
解:(1)设AB为点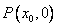 的任意一条“相关弦”,且点A、B的坐标分别是
的任意一条“相关弦”,且点A、B的坐标分别是
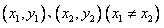
则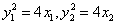
两式相减得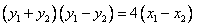
因为x1≠x2
所以y1+y2≠0
设直线AB的斜率是k,弦AB的中点是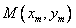 ,则
,则
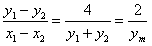
从而AB的垂直平分线l的方程为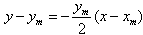
又点P(x0,0)在直线上,
所以
而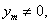 于是
于是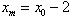
故点P(x0,0)的所有“相关弦”的中点的横坐标都是x0-2;
(2)由(1)知,弦AB所在直线的方程是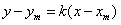 ,代入
,代入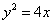 中
中
整理得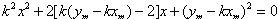 (·)
(·)
则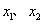 是方程(·)的两个实根,且
是方程(·)的两个实根,且
设点P的“相关弦”AB的弦长为l,则

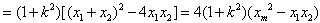
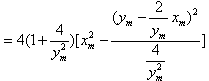


因为
于是设t=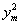 ,则t∈(0,4x0-8)
,则t∈(0,4x0-8)
记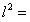
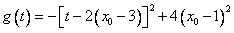
若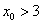 ,则
,则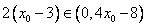
所以当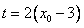 ,即
,即 =2(x0-3)时,l有最大值
=2(x0-3)时,l有最大值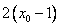
若 ,则
,则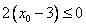 ,
,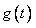 在区间
在区间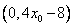 上是减函数
上是减函数
所以 ,l不存在最大值
,l不存在最大值
综上所述,当x0>3时,点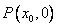 的“相关弦”的弦长中存在最大值,且最大值为2(x0-1);当2<x0≤3时,点
的“相关弦”的弦长中存在最大值,且最大值为2(x0-1);当2<x0≤3时,点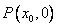 的“相关弦”的弦长中不存在最大值。
的“相关弦”的弦长中不存在最大值。
