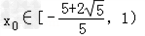问题
解答题
已知直线l：y=kx+k+1，抛物线C：y2=4x，定点M（1，1）．
（I）当直线l经过抛物线焦点F时，求点M关于直线l的对称点N的坐标，并判断点N是否在抛物线C上；
（II）当k（k≠0）变化且直线l与抛物线C有公共点时，设点P（a，1）关于直线l的对称点为Q（x0，y0），求x0关于k的函数关系式x0=f（k）；若P与M重合时，求x0的取值范围．
答案
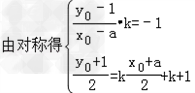
解：（I）由焦点F（1，0）在l上，得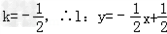
设点N（m，n）则有：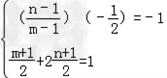
，
解得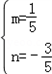
，
∴
∵
，
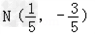
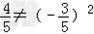N点不在抛物线C上．
（2）把直线方程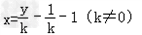
代入抛物线方程得：ky2﹣4y+4k+4=0，
∵相交，∴△=16（﹣k2﹣k+1）≥0，
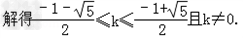
解得
．
当P与M重合时，a=1
∴
，
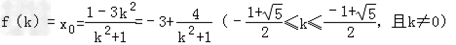∵函数x0=f（x）（k∈R）是偶函数，且k＞0时单调递减．
∴
，
，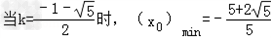
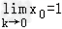