问题
解答题
已知关于x的方程
(1)当k=-1时,该方程的根是______; (2)当k≠-1时,该方程有两个不相等的实数根吗?并说明理由. |
答案
(1)当k=-1时,方程化为
x2-2x+4=0,1 4
整理得x2-8x+16=0,
∴(x-4)2=0,
∴x1=x2=4;
故答案为x1=x2=4;
(2)当k≠-1时,该方程有两个不相等的实数根.
理由如下:
△=(k-1)2-4×
×(-4k)=(k+1)2,1 4
∵k≠-1,即k+1≠0,
∴(k+1)2>0,即△>0,
∴,方程有两个不等实根.

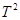 为纵坐标,将所得数据连成直线如图B所示,利用图像可求出重力加速度g=_______
为纵坐标,将所得数据连成直线如图B所示,利用图像可求出重力加速度g=_______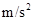 。(结果保留三位有效数字)
。(结果保留三位有效数字)