问题
解答题
在平面直角坐标系xOy中,过定点C(0,p)作直线与抛物线x2=2py(p>0)相交于A、B两点。
(1)若点N是点C关于坐标原点O的对称点,求△ANB面积的最小值;
(2)是否存在垂直于y轴的直线l,使得l被以AC为直径的圆截得弦长恒为定值?若存在,求出l的方程;若不存在,说明理由。
答案
解:(1)依题意,点N的坐标为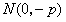 ,
,
可设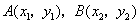
直线AB的方程为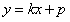 ,与
,与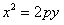 联立得
联立得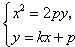
消去y得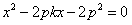
由韦达定理得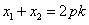 ,
,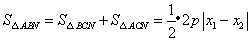
于是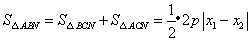
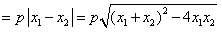
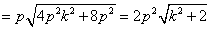
∴当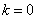 时,
时, 。
。
(2)假设满足条件的直线l存在,其方程为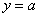 ,
,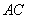 的中点为
的中点为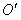 ,
,
l与AC为直径的圆相交于点P,Q,
PQ的中点为H,
则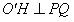 ,
,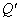 点的坐标为
点的坐标为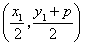
∵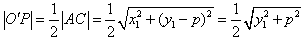 ,
,
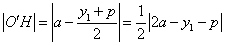 ,
,
∴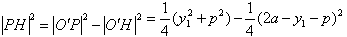 ,
,
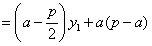
∴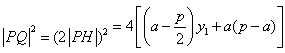
令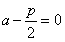 ,得
,得 ,此时
,此时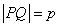 为定值,
为定值,
故满足条件的直线l存在,其方程为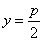 ,
,
即抛物线的通径所在的直线。
