问题
解答题
已知抛物线y2=2px(p>0),其焦点为F,一条过焦点F,倾斜角为θ(0<θ<π)的直线交抛物线于A、B两点,连接AO(O为坐标原点),交准线于点B′,连接BO,交准线于点A′,求四边形ABB′A′的面积。
答案
解:当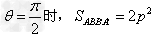 ;
;
当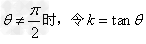 ,
,
设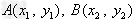 ,
,
则由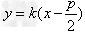 , ①
, ①
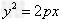 , ②
, ②
消去x得,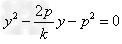 ,
,
所以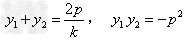 , ③
, ③
又直线AO的方程为: ,
,
所以,AO与准线的交点的坐标为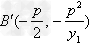 ,
,
而由③知,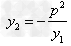 ,
,
所以B和B′的纵坐标相等,
从而BB′∥x轴,同理AA′∥x轴,
故四边形ABB′A′是直角梯形,
所以,它的面积为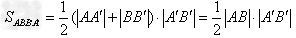
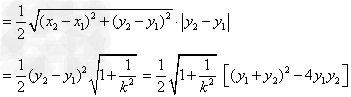
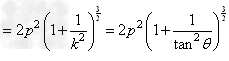 。
。
