问题
解答题
设A （x1 ，y1 ），B （x2 ，y2）为抛物线y2=2px（p>0）上位于x 轴两侧的两点．
（1）若y1y2=-2p ，证明直线AB 恒过一个定点；
（2）若p=2 ，∠AOB（O为坐标原点）为钝角，求直线AB 在x轴上截距的取值范围．
答案
（1）证明：设直线AB在x轴上的截距为t，直线AB的方程为x=my+t，代人y2=2px（p>0），得y2=2p（my+t），即y2-2pmy-2pt=0，
于是-2p=y1y2=-2pt，所以t=1，
即直线AB恒过定点（1，0）．
（2）解：∠AOB（O为坐标原点）为钝角，
∴
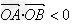，即x1x2+y1y2<0．
∵
∴
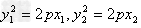
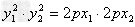
于是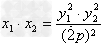
由（1）得y1·y2=-2pt，
∴
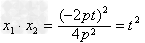
又p=2，
∴x1x2+y1y2=t2-2pt=t2-4t<0
解得0<t<4，
即直线AB在x轴上的截距的取值范围是（0，4）．