问题
解答题
已知抛物线y2=4x,焦点为F,顶点为O,点P在抛物线上移动,Q是OP的中点.
(1)求点Q的轨迹方程;
(2)若倾斜角为60°且过点F的直线交Q的轨迹于A,B两点,求弦长|AB|.
答案
解:(1)设Q(x,y),
∵Q是OP中点,
∴P(2x,2y)
又∵点P在抛物线y2=4x上
∴(2y)2=4×2x,
即y2=2x为点Q的轨迹方程
(2)∵F(1,0),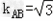 ,
,
∴直线AB的方程为: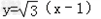
设点A(x1,y1),B(x2,y2)
直线AB的方程代入y2=2x,
消去y得:3x2﹣8x+3=0
∴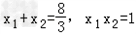
∴