问题
解答题
观察下列等式
(1)猜想并写出:
(2)直接写出下列各式的计算结果: ①
②
(3)探究并计算:
|
答案
(1)
-1 n
;1 n+1
(2)①原式=1-
+1 2
-1 2
+1 3
-1 3
+…+1 4
-1 2012
=1-1 2013
=1 2013
;2012 2013
②原式═1-
+1 2
-1 2
+1 3
-1 3
+…+1 4
-1 n
=1-1 n+1
=1 n+1
;n n+1
(3)原式=
(1 4
+1 1×2
+1 2×3
+…+1 3×4
)1 1006×1007
=
(1-1 4
)1 1007
=
.503 2014
故答案为
-1 n
;1 n+1
;2012 2013
.n n+1

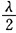 (λ为波长)的两点的振动速度必定()。
(λ为波长)的两点的振动速度必定()。