问题
解答题
已知直线x+y=1过抛物线y2=2px的焦点F．
（1）求抛物线C的方程；
（2）过点T（﹣1，0）作直线l与轨迹C交于A，B两点若在x轴上存在一点E（x0，0），使得△ABE是等边三角形，求x0的值．
答案
解：（1）直线x+y=1与x轴交于（1，0）
∵直线x+y=1过抛物线y2=2px的焦点F
∴抛物线的焦点为F（1，0），故p=2
∴抛物线C的方程为y2=4x．
（2）设直线l：y=k（x+1）（k≠0）
代入y2=4x（x＞0），
消元可得k2x2+2（k2﹣2）x+k2=0，
设A（x1，y1），B（x2，y2），
则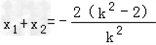
，x1x2=1，
∴AB的中点为
，
∴线段AB的垂直平分线方程为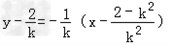
，
令y=0，得
∵△ABE是等边三角形，
∴点E到直线l的距离为
，
∵点E到直线l的距离为
，
，
∴
∴
∴
．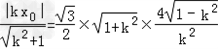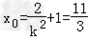