问题
解答题
在平面内,设到定点F(0,2)和x轴距离之和为A的点P轨迹为曲线C,直线l过点F,交曲线C于M,N两点.
(Ⅰ)说明曲线C的形状,并画出图形;
(Ⅱ)求线段MN长度的范围。
答案
解:(Ⅰ)设动点P(x,y),由已知得: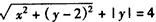 ,
,
当y≥0时,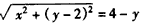 ,化简,得
,化简,得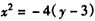 ;
;
当y≤0时,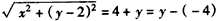 ,化简,得x2=12(y+l),
,化简,得x2=12(y+l),
∴如图:曲线C是焦点在F(0,2),准线分别为y=-4和y=4,顶点分别是(0,-1)和(0,3)的两条抛物线一部分组成的封闭图形ABCD,
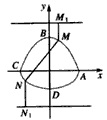
(Ⅱ)当M,N在两支抛物线上时,过M,N分别作相应准线的垂线,垂足分别是M1,N1,
由抛物线定义,MM1=MF;NN1=NF,
设M,N的纵坐标分别为y1,y2,|MN|=8-(|y1|+|y2|),
当l过BD时, |MN|最小,最小值为4,
当l过C(或A)时,|MN|最大,
此时直线l的方程为-x+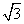 y=2
y=2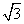 和抛物线x2=-4(y-3),
和抛物线x2=-4(y-3),
另一交点 ,|MN|最大值为
,|MN|最大值为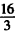 ,|MN|范围是
,|MN|范围是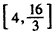 ,
,
当M.N都在上支抛物线上时,易求|MN|范围也是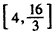 ;
;
∴综上所述,|MN|范围是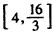 。
。
