问题
解答题
(1)已知f(2x+1)=3x-2且f(a)=4,求a的值;
(2)已知f(x)=ax2+bx+c,若f(0)=0,且f(x+1)=f(x)+x+1,求f(x)的解析式.
答案
解:(1)∵f(2x+1)=3x-2=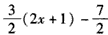 ,
,
∴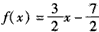 ,
,
∴f(a)=4,即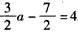 ,
,
∴a=5。
(2)∵f(0)=c=0,
∴f(x+1)=a(x+1)2+b(x+1)+c=ax2+(2a+b)x+a+b,
f(x)+x+1=ax2+bx+x+1=ax2+(b+1)x+1,
∴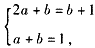 ,∴
,∴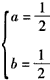 ,
,
∴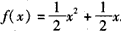 。
。
