问题
解答题
已知二次函数f(x)满足f(x+1)-f(x)=2x且f(0)=1.
(1)求f(x)的解析式;
(2)当x∈[-1,1]时,不等式:f(x)>2x+m恒成立,求实数m的范围.
(3)设g(t)=f(2t+a),t∈[-1,1],求g(t)的最大值.
答案
(1)令f(x)=ax2+bx+c(a≠0)代入f(x+1)-f(x)=2x,
得:a(x+1)2+b(x+1)+c-(ax2+bx+c)=2x,2ax+a+b=2x,
∴
,a=1 b=-1 c=1
∴f(x)=x2-x+1;
(2)当x∈[-1,1]时,f(x)>2x+m恒成立即:x2-3x+1>m恒成立;
令g(x)=x2-3x+1=(x-
)2-3 2
,5 4
x∈[-1,1],
则对称轴:x=
∉[-1,1],3 2
则g(x)min=g(1)=-1,
∴m<-1;
(3)g(t)=f(2t+a)=4t2+(4a-2)t+a2-a+1,t∈[-1,1]
对称轴为:t=
,1-2a 4
①当
≥0时,即:a≤1-2a 4
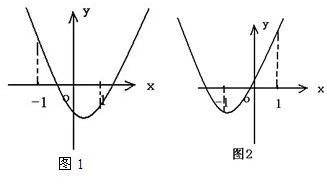
;如图1:1 2
g(t)max=g(-1)=4-(4a-2)+a2-a+1=a2-5a+7
②当
<0时,即:a>1-2a 4
;如图2:1 2
g(t)max=g(1)=4+(4a-2)+a2-a+1=a2+3a+3,
综上所述:g(t)max=a2-5a+7 a2+3a+3
.a≤ 1 2 a> 1 2